学习周报第三周
霍普菲尔德网络学习周报
遗留问题解决
1.为什么霍普菲尔德网络不能处理异或问题?
霍普菲尔德网络不能处理异或问题是因为异或是一个非线性可分问题,而霍普菲尔德网络本质上是一种线性模型,无法通过简单的线性组合来区分异或问题中不同的输入组合所对应的输出类别。
注释:
- 什么是异或
异或(XOR)是一个经典的二元逻辑运算,其真值表如下:
| 输入 A | 输入 B | 输出 (A XOR B) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
- 线性可分、线性不可分
线性可分:如果在一个特征空间中,能够找到一个超平面(hyperplane)将不同类别的样本点完全地分开,那么这些样本就是线性可分的。
二维空间:超平面为直线。
三维空间:超平面为平面。
更高维度空间: 超平面是高维的线性边界
例如:
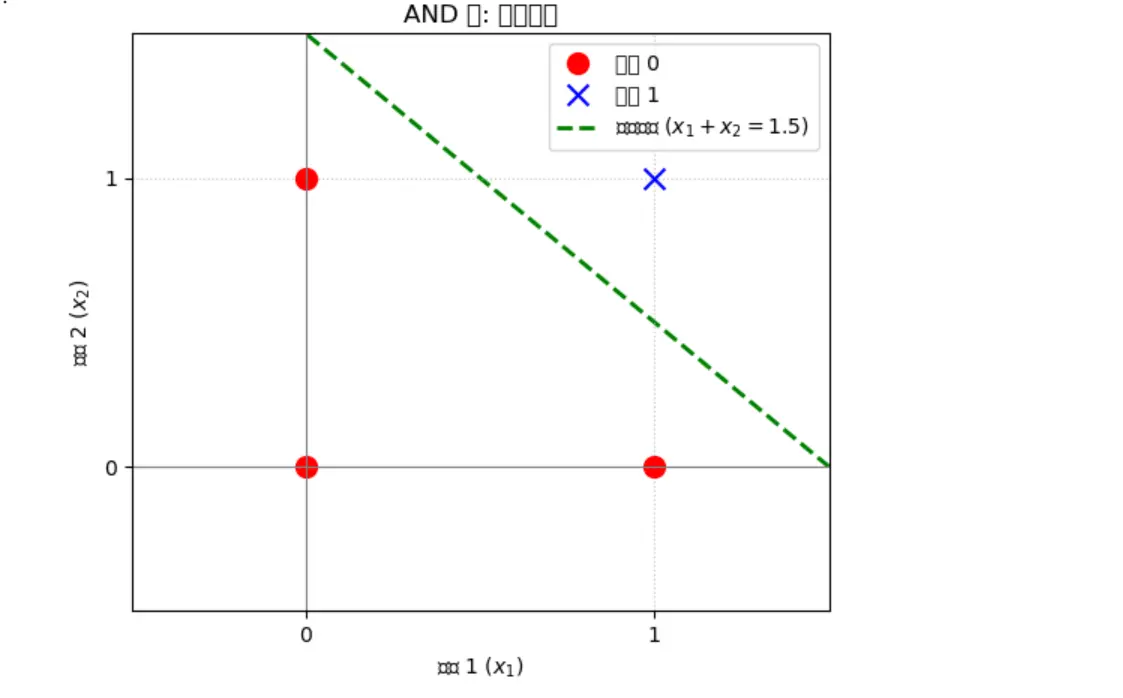
一个简单的AND门问题:
- (0,0) -> 0
- (0,1) -> 0
- (1,0) -> 0
- (1,1) -> 1
绿线将两类点完全分开。
线性不可分:如果在一个特征空间中,无法找到一个超平面将不同类别的样本点完全地分开,那么这些样本就是线性不可分的。
例如:
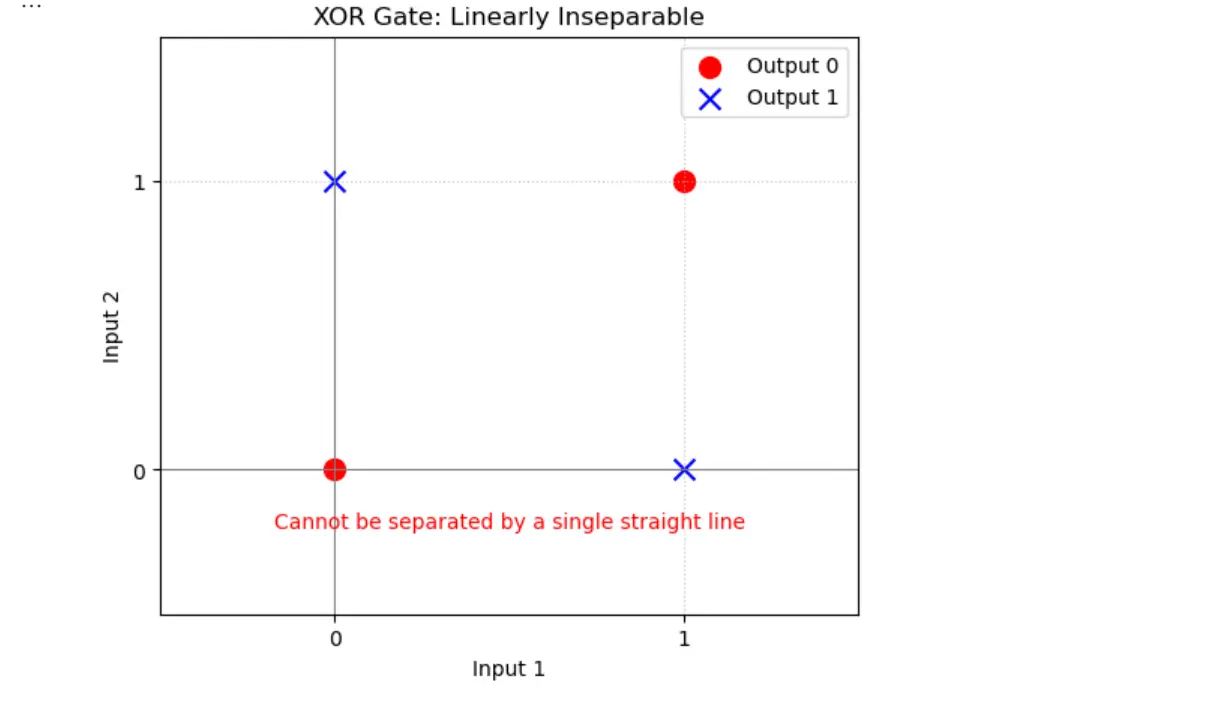
异或(XOR)问题:
- (0,0) -> 0
- (0,1) -> 1
- (1,0) -> 1
- (1,1) -> 0
没有线可以将两类点分开。
- 为什么无法处理异或问题
霍普菲尔德网络中单个神经元的状态更新依据其净输入: 。神经元 i 的新状态将根据 hi 的正负号(例如,若 hi≥0 则为 +1,若 hi<0 则为 −1)来确定。但是当hi=0的时候,这个方程定义了一个线性决策边界(在多维输入空间中表现为一个超平面)。这意味着,无论网络如何通过学习调整权重 Wij,每个神经元在决定自身状态时,都只能通过一个线性的“切割”来区分其输入模式。然而,异或 (XOR) 问题本质上是线性不可分的。它的输入-输出模式无法通过单一的直线(或更高维度的超平面)在原始输入空间中被完全区分开来。
2.如何在霍普菲尔德网络中存储多个模式
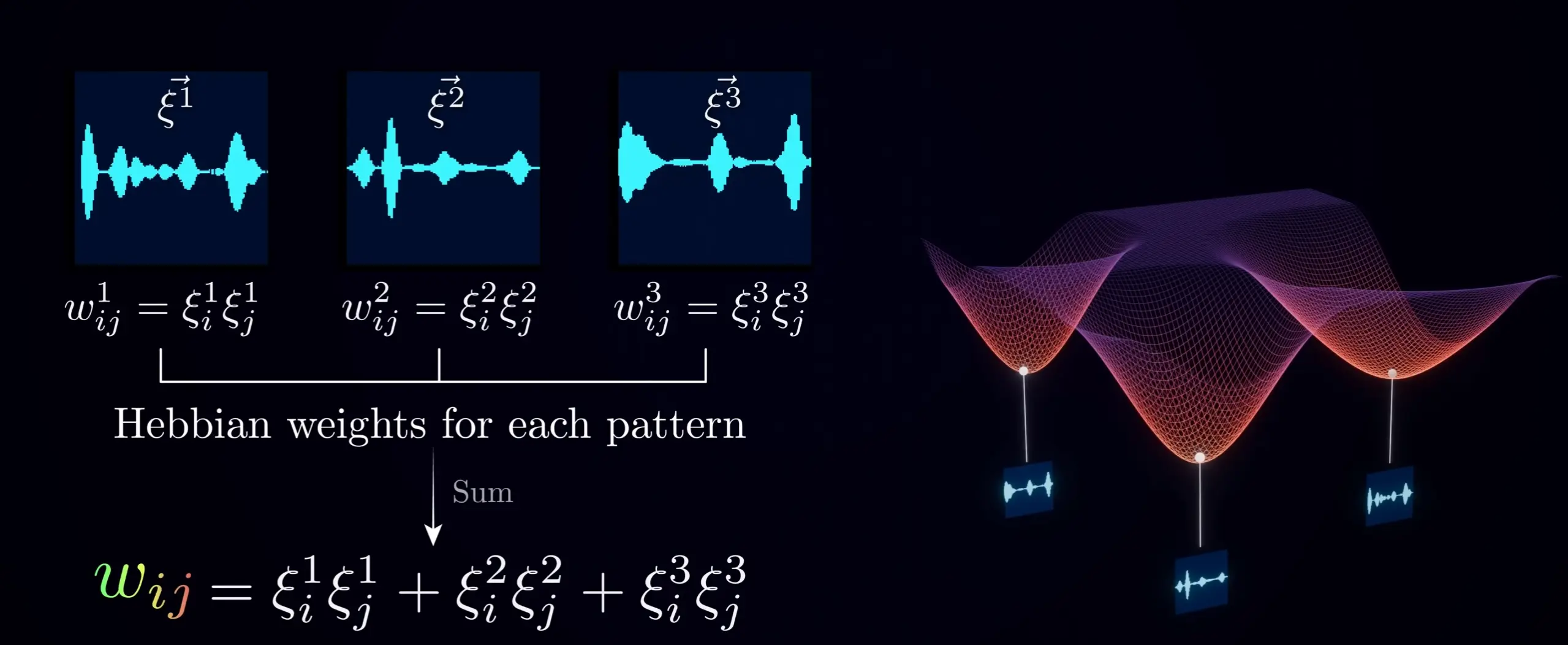
- 我们可以简单的将每个模式叠加在一起,根据以下等式计算权重。
这将把每一个模式都变成局部最小值,具体的内容可以阅读文献来获取答案。
Hopfield Networks: Neural Memory Machines | Towards Data Science
Hopfield Networks is All You Need | hopfield-layers
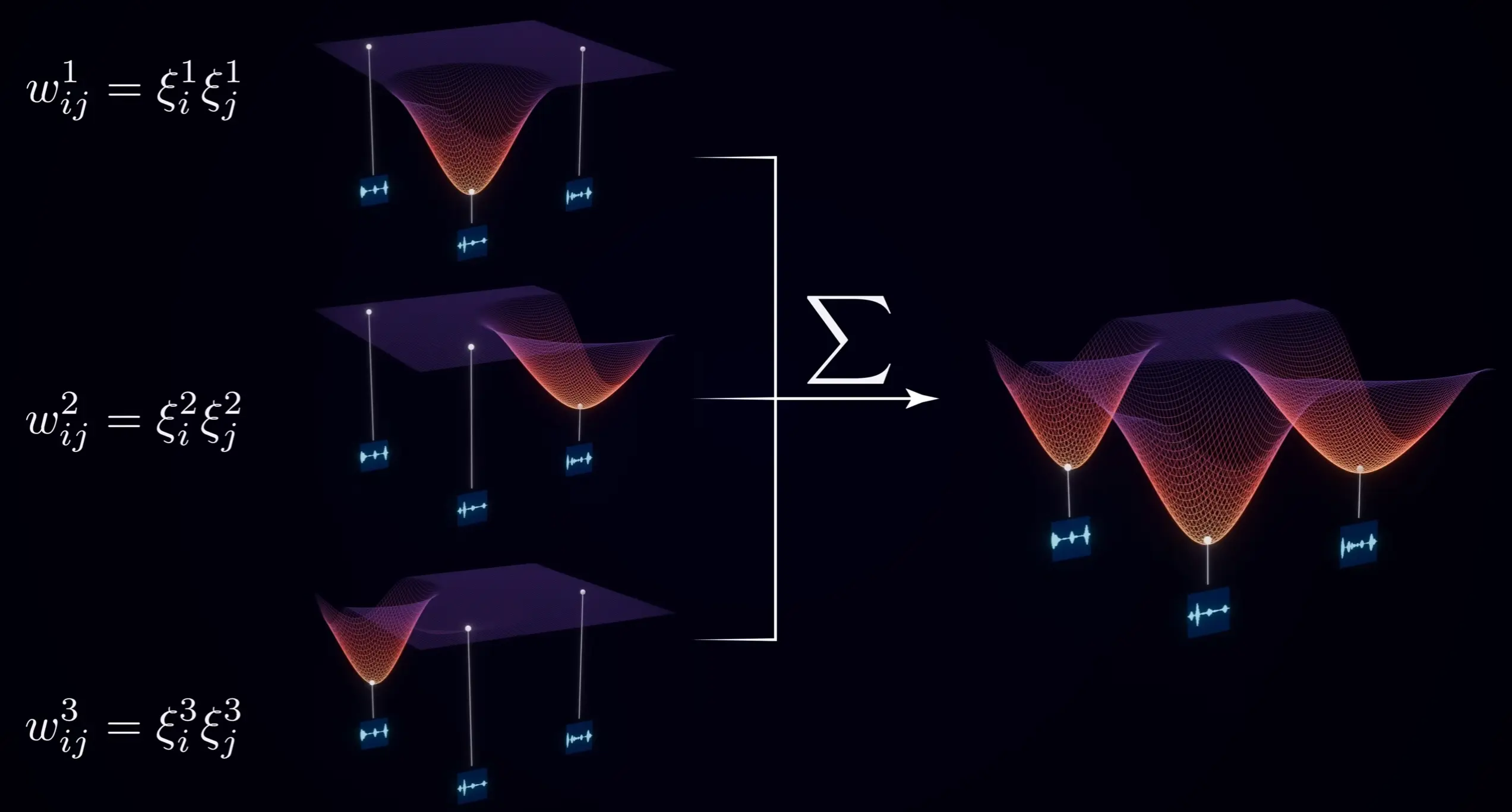
- 为每个模式独立的挖掘能量井,然后将能量景观叠加在一起。
这进而引出了或普菲尔德网络的局限性:
在网络中,我们能塑造的能量谷是有限的,如果我们存储过多的模式,那么我们将无法可靠的收敛到储存的模式,甚至出现奇怪的中间记忆,这个模式的数量取决于神经网络的数量,大约是神经原网络的0.14倍。
但是如果两个模式有很强的相似性或者相关性,那么他们会在达到最大模式存储数量之前,就会产生干扰。
进度
截至2025年5月25日,完成了霍普菲尔德网络的学习。按照进度,下周将完成霍普菲尔德网络的代码编写和第一篇论文的解读。
心得
1.随着不断学习,越来越发现,自身所了解的很少,在学习新知识的时候,所学的知识也在不断地拓展、闭环。也有了迫切的学习新的知识,来搭建自己完整的知识网络的热情。
2.构建霍普菲尔德网络本质上两个步骤
- 构建能量景观
- 创建类似热力学第二定律的推进模式
问题
在拓展探讨中,显示了两种存储,简单理解为开存储和叠加存储,他们的存储模式的数量大约是神经原网络的0.14倍。这个都使用吗?是怎么得出的?为什么叠加存储不能有更多数量的存储模式?
总结
详细内容在博客:霍普菲尔德网络 | moshiqiqian