学习周报第八周

QDA学习

QDA

1、思想总结：

优化算法迭代过程中，解的概率演化过程被量子动力学方程转化为了波函数模方的演化过程，目标函数的全局最小值问题在量子动力学方程下被转化为了基态波函数模方问题。

注释：把优化算法寻优的过程比作量子力学中，寻找基态波函数的过程。

2、理论支撑：

因为在优化算法中我们通常将目标函数f（x） 视为黑盒函数，因此并不能通过求解优化算法的量子动力学方程来获得基态波函数的模方，而且薛定谔方程十分复杂。所以我们将方程中的目标函数分别进行零阶、一阶和二阶Taylor近似，通过不同的近似来剥离优化算法的基本迭代操作。

注释：

1.在实际情况下，目标函数是通过采样来估计的（未知的），泰勒展开只应用于其对应的理论支撑。

2.简单来说，我们根据目标函数的泰勒展开后的数学公式的性质，对应到了，实际上在量子动力学下的实际情况。

3、泰勒展开解释：

（1）零阶泰勒展开：当目标函数近似为常数时，在量子力学中，这对应于自由粒子的状态 。

注释：

这个类比的核心逻辑是：

• 泰勒展开的性质：
  • 当对目标函数进行零阶泰勒展开时，我们是在说，在某一个局部区域内，函数可以被近似为一个常数。
  • 这个“常数”的性质，在数学上意味着函数是平坦的，没有斜率，没有变化趋势。
• 量子力学的性质：
  • 在量子力学中，自由粒子的定义就是不受任何力或势能场影响的粒子。
  • 这意味着它的**势能是恒定（常数）**的，也就是平坦的。

（2）一阶泰勒展开：当目标函数近似为线性斜坡时，在量子力学中，这对应于粒子遇到势垒的情景 。

注释：

我们可以这样更具体地来阐述：

• 泰勒展开的：

  • 一阶泰勒展开：f(x)≈f(x0)+f′(x0)(x−x0)
  • 斜率：这个公式中的 f′(x0) 就是函数在 x0 点的一阶导数。它代表了函数在这个点变化的方向和速率。
  • “线性斜坡”：从几何上看，这个展开式就是用一条切线（一个斜坡）来近似函数在 x0 附近的行为。

• 量子动力学：

  • 粒子：你的“行走者”。
  • 运动：粒子会倾向于从高能态（山峰）移动到低能态（山谷）。

总而言之：一阶导数反应函数的变化趋势，如果为正数，那么函数值整体呈上升的状态，反应了收敛过程中的能量值上升，以此类比下降。它可以很好的“指导”粒子的运动。；同时上升的斜坡类似于“壁垒”，有直觉上有很好的相似性。

（3）二阶泰勒展开：当目标函数在极值点附近近似为二次函数时，在量子力学中，这对应于量子谐振子的基态状态 。

注释：

我们可以这样联系

数学方面：

二阶近似：当我们只取到二阶项时，得到的公式是：

$f(x) \approx f(x_0) + f'(x_0)(x-x_0) + \frac{1}{2}f''(x_0)(x-x_0)^2$

在极值点：如果 x0 是一个局部极值点，那么函数的一阶导数 f′(x0) 必须为零。所以公式简化为：

$f(x) \approx f(x_0) + \frac{1}{2}f''(x_0)(x-x_0)^2$

而量子谐振子的势能函数

$V(x) = \frac{1}{2}m\omega^2(x-x_0)^2$

你会发现这个势能函数的数学形式与上面泰勒二阶近似的公式完全一致
​
在性质上：

• 优化算法中的“极值点” <=>量子力学中的“基态”
  • 优化算法的目标是找到最小值。
  • 量子谐振子的目标是达到能量最低的基态。
• 粒子群体在极值点附近的行为<=> 基态波函数的正态分布
  • 在优化算法中，当粒子群体收敛到极值点附近时，它们会紧密地聚集在一起。
  • 在量子谐振子的基态，粒子的波函数模方是正态分布，这意味着粒子最有可能出现在势能场的最低点，而在远离最低点的地方，出现的概率很低。

4、代码详解：

def func1(matrix_y):# y=x*x
    y=0
    for i in matrix_y:
        y+=i*i
    return y

matrix_y：代表着NumPy 数组。
在其中的循环中，i代表着这数组的一行。
一个简单的抛物线函数。

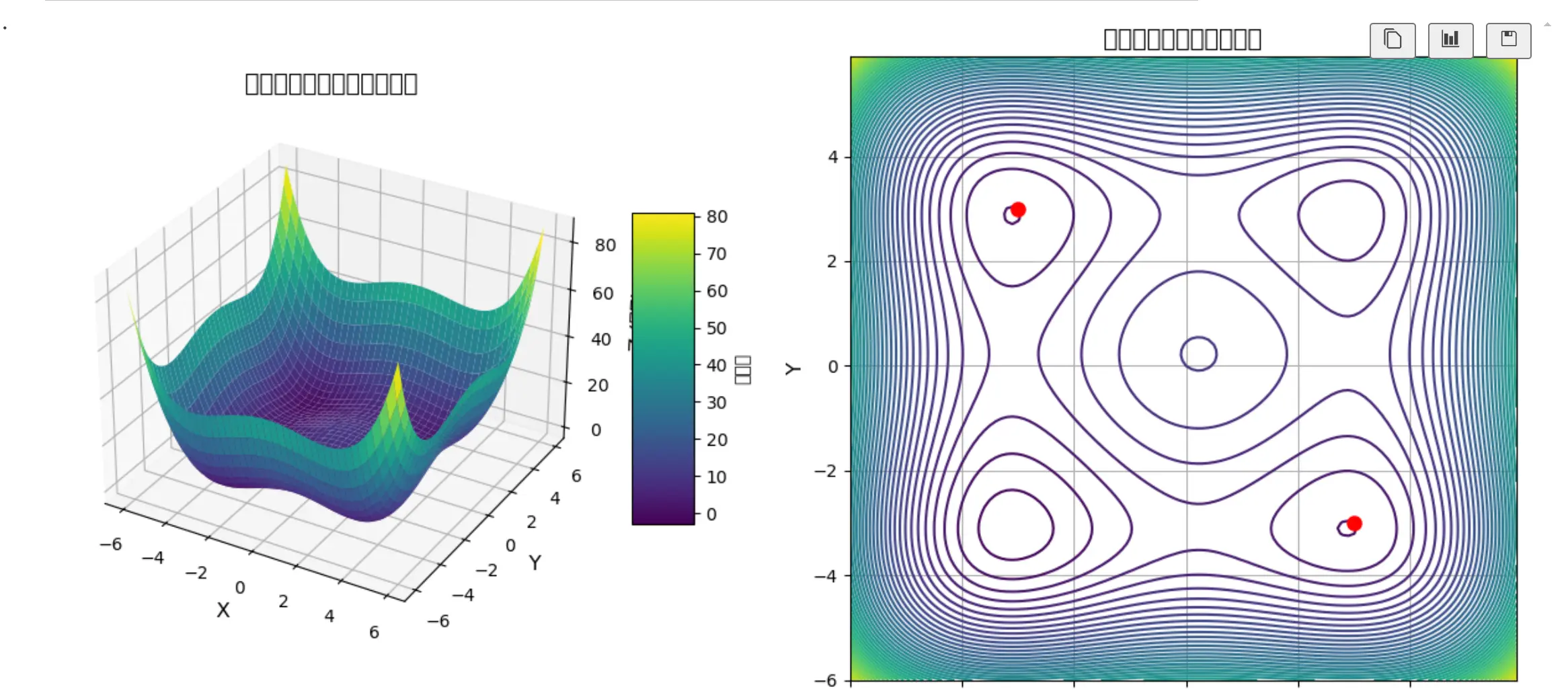
def func(matrix_y):    #double well function
    y=0
    l,k,h=3.0,0.5,5.0
    for i in matrix_y:
        y+=h*pow((pow(i, 2)-pow(l, 2)), 2)/pow(l, 4)+k*i
    return y

pow(x,y)：代表着x^y。
是一个双井函数大致图像如下。

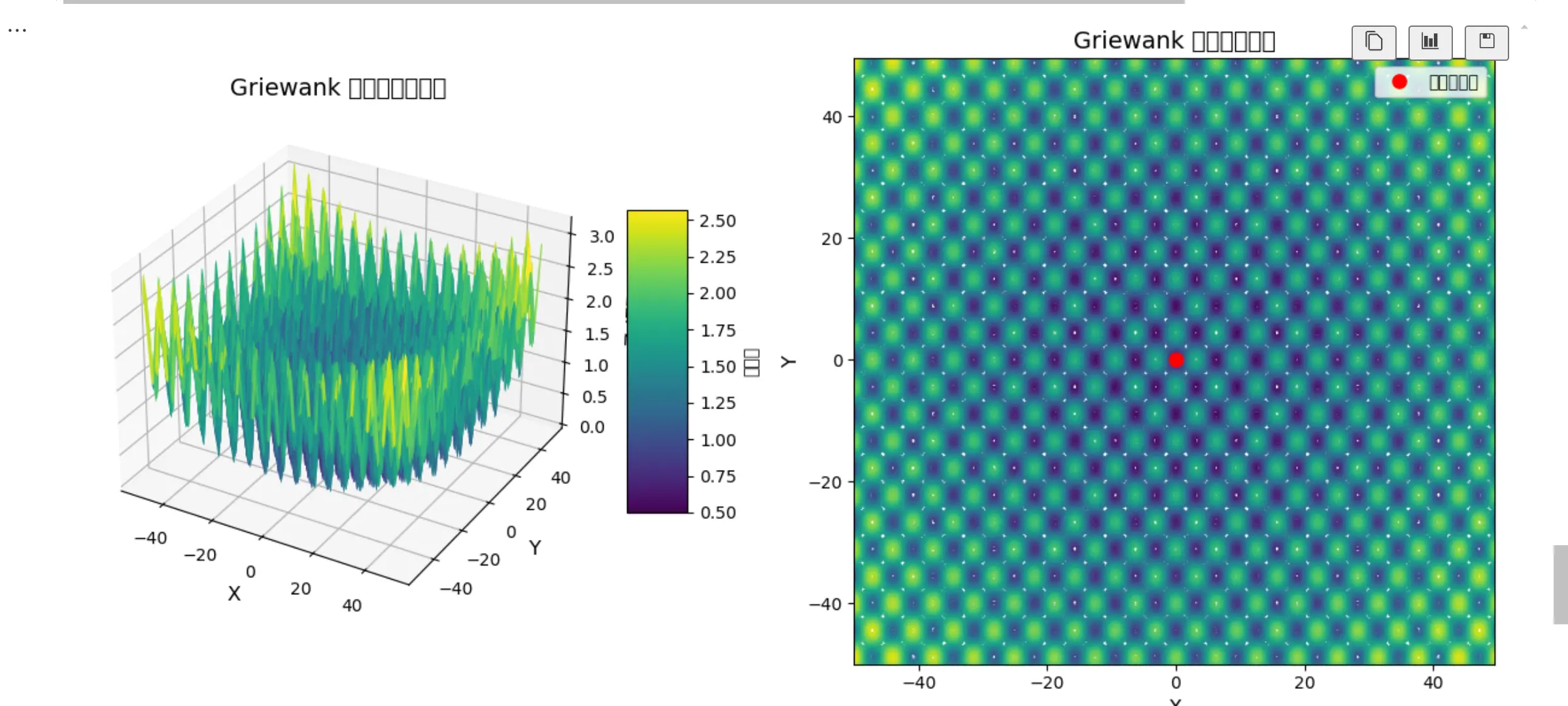
def func1(matrix_y):    #Griewank
    a,b,y=0,1,0
    index=1
    for i in matrix_y:
        a=a+i*i
        b=b*np.cos(i/np.sqrt(index))
        index+=1
    y=1+1/4000*a-b
    return y

def mid_exchange(matrix):
    mid_walker=np.mean(matrix,1)
    matrix[:,max_min_id(matrix,0)]=mid_walker
    return matrix

np.mean：计算平均值，如果只有一个数组（参数），那么直接计算其中的平均值。如果有两个参数例如np.mean(x,y)，x代表数组，y = 0/1。y = 0按照列来计算平均值，y = 1按照行来计算平均值。
本质上是找到坐标中的中心点，代表行走者在维度上的平均位置。

def max_min_id(matrix,flag): #obtain max or min walker's index
    walker_id=0
    temp=func(matrix[:,0])
    for j in range(walker_n-1):
        if temp < func(matrix[:, j + 1]) and flag == 0:#max condition
            walker_id = j + 1
            temp = func(matrix[:, j + 1])
        if temp > func(matrix[:, j + 1]) and flag == 1:#min condition
            walker_id = j + 1
            temp = func(matrix[:, j + 1])
    return walker_id

matrix: 这是一个 (dim, walker_n) 的二维数组，代表了所有行走者的坐标。
flag：0->最大值,1->最小值。
本质上是为了寻找最大值和最小值。

acc=0.000001
ite_times=0
dim, walker_n=2, 20
begin, end=-6, 6
scale=end-begin
ite_flag=True       
a=np.random.uniform(begin, end, (dim, walker_n))
b=np.zeros((dim,walker_n))

acc:精度，当scale小于这个尺度的时候，停止。
ite_times:计数器，记录迭代次数。
dim:维度。 walker_n :行走者数量。这两个综合起来代表坐标(X,Y)。
begin, end:坐标都将被限制在 [-6, 6]。
scale:是尺度或搜索范围。
ite_flag:True表示内层循环将继续运行；False 表示内层循环将停止。
a:代表代表了所有行走者当前的位置。这行代码的作用是随机初始化20个行走者，将它们分散在 [-6, 6] 的搜索空间中。
np.random.uniform(low, high, size) 是 NumPy 的一个函数，用于生成在 [low, high) 范围内的均匀分布随机数。
b:b 是一个临时数组，用于存储新的采样位置。

while scale>acc:
    while ite_flag==True:
        ite_times+=1
        for j in range(walker_n):
            for i in range(dim):
                b[i, j]=np.random.normal(a[i, j], scale) #sampling
                while b[i,j]<begin or b[i, j]>end:
                    b[i,j] = np.random.normal(a[i, j], scale)
            if func(b[:,j])>func(a[:, j]):
                b[:, j]=a[:, j]
        mid_exchange(b)  #mean value replacement function.
        a[:, :] = b[:, :]
        ite_flag=False
        for i in range(dim):
            if np.var(a[i, :]) > pow(scale, 2):
                ite_flag=True
    scale=scale/2
    print(scale)
    ite_flag=True

外层循环：

while scale>acc:
……
scale=scale/2
    print(scale)
    ite_flag=True

控制循环，使精度逐渐上升。

内层循环：

while ite_flag==True:
        ite_times+=1
        for j in range(walker_n):
            for i in range(dim):
                b[i, j]=np.random.normal(a[i, j], scale) 
                while b[i,j]<begin or b[i, j]>end:
                    b[i,j] = np.random.normal(a[i, j], scale)
            if func(b[:,j])>func(a[:, j]):
                b[:, j]=a[:, j]
        mid_exchange(b)  #mean value replacement function.
        a[:, :] = b[:, :]
        ite_flag=False
        for i in range(dim):
            if np.var(a[i, :]) > pow(scale, 2):
                ite_flag=True

b[i, j]=np.random.normal(a[i, j], scale) 按照正态分布随机生成一个新的坐标。
while b[i,j]<begin or b[i, j]>end: 判断是否在边界之内。
if func(b[:,j])>func(a[:, j]): 进行新旧值的数值对比，决定是否更新。
mid_exchange(b):均值替换。
a[:, :] = b[:, :]将更新后的b赋值到a。

ite_flag=False
        for i in range(dim):
            if np.var(a[i, :]) > pow(scale, 2):
                ite_flag=True

判断是否收敛。

5、哪里体现了量子动力学

（1）他没有确定为一个确定的坐标，反而是用正态分布来随机取样，符合量子力学中的概率分布（位置的不确定性）。

（2）使用了退火策略：粒子倾向于处于最低能量状态。在温度较高时，粒子更加活跃，位置更新的范围更大；在温度较低时，粒子较稳定，位置更新范围小。

scale 参数可以类比为“温度”

问题

为什么qda会如此高效，黑盒状态下的算法，该如提升性能？

高斯采样，限制采样的范围，贪心，退火范围，
多尺度，均值替换。

我接下来的学习方向？论文选题的方向？

conda qda算法，量子隧穿，并行的策略，为什么qda没有差分进化快。